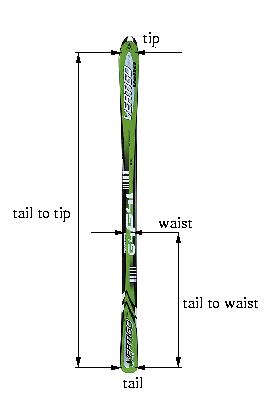
To do this accurately you need to know the max width at the tip, the waist width and the max width at the tail. You also need to know the distance from the tail widepoint to the waist and to the tip widepoint. Note that the sidecut radius of a ski need not exist. More exactly put, not every sidecuts is a circular arc. However, my formula calculates the radius of the uniquely defined circle that passes through the three defining points, and hence the number you get is a good approximation of the truth in general.

|
|
|
Tail to tip (mm) |
|
|
Waist width (mm) |
|
|
Tail to waist (mm) |
|
|
Tail width (mm) |
|
Sidecut radius i meters |
| Model | Tip (mm) | Tail to tip (mm) | Waist (mm) | Tail to waist (mm) | Tail (mm) | Sidecut radius (m) |
| V�lkl G41 198 | 117 | 1750 | 83 | 800 | 105 | 27.7 |
| V�lkl P30 RC Racing "rennservice" 203 | 98.5 | 1810 | 62 | 770 | 84 | 28.5 |
Do you want to know what the formula look like? Well, denote tail width with tail, waist width with w, tip width with tip, tail to tip with tt and tail to waist with tw, then the sidecut radius is given by:
radius=1/1000*sqrt(-((((tail-w)/2)^2*((tail-w)/2*tt-(tip-w)/2*tw)-(tw^2)*((tail-w)/2*tt)+ (tw^2)*((tail-w)/2*tw))/(-(tip-w)/2*tw-(tail-w)/2*tt+(tail-w)/2*tw)-(((tw^2)*tt -(((tip-w)/2)^2+tt^2)*tw -(((tail-w)/2)^2)*tt +((tail-w)/2)^2*tw)/(2*(-(tip-w)/2*tw-(tail-w)/2*tt+(tail-w)/2*tw)))*(((tw^2)*tt -(((tip-w)/2)^2+tt^2)*tw -(((tail-w)/2)^2)*tt +((tail-w)/2)^2*tw)/(2*(-(tip-w)/2*tw-(tail-w)/2*tt+(tail-w)/2*tw)))-((tw^2*(tip-w)/2 -((tail-w)/2)^2*(tip-w)/2 +(((tip-w)/2)^2+tt^2)*(tail-w)/2-(tw^2)*(tail-w)/2)/(2*(-(tip-w)/2*tw-(tail-w)/2*tt+(tail-w)/2*tw)))*((tw^2*(tip-w)/2 -((tail-w)/2)^2*(tip-w)/2 +(((tip-w)/2)^2+tt^2)*(tail-w)/2-(tw^2)*(tail-w)/2)/(2*(-(tip-w)/2*tw-(tail-w)/2*tt+(tail-w)/2*tw)))));